Hybrid Hierarchical Deterministic Wallets

A Hybrid Hierarchical Deterministic wallet uses a single seed phrase to securely derive both traditional crypto keys and post-quantum keys, combining familiar HD wallet standards with future-proof cryptography for long-term blockchain security.

Introduction

TL;DR

In this blogpost we present a hybrid design for a hierarchical deterministic wallet derived from a single seed phrase, that supports both post-quantum and non-post-quantum (a.k.a. classical) signatures.

We open-sourced a Rust implementation, which you can check in our Bedrock repo, and its specification in the hhd-spec repo.

Author: Manuel B. Santos manuel@tectonic.xyz

Motivation

Managing secret keys has always been one of the biggest pain points in crypto. Thankfully, over time, some BIP standards made this task easier and safer.

BIP-32 introduced hierarchical deterministic (HD for short) wallets, providing a way to derive an entire tree of keys from a single master key. BIP-44 then standardized derivation paths so wallets could work across different providers, and BIP-39 added mnemonic seed phrases that made backups simple: you just need to remember a few words to recover everything. These improvements definitely made wallets more user-friendly and interoperable.

BIP-32 also introduced two types of derivation: hardened and non-hardened. The former is usually used when we need total isolation between keys, such that leaking a child key does not compromise higher levels. The latter is crucial for generating public keys without private ones that is perfect for watch-only wallets or payment processors. Indeed, this approach powers real-world setups like Blue Wallet or Blockstream Wallet, which can monitor balances without knowing the private keys; and BitPay Wallet or BTCPay, which can generate addresses securely from a master extended public key.

All these standards were initially designed with ECDSA in mind and SLIP-10 extended the idea to other algorithms like EdDSA. But with quantum computing and the Q-Day [1] on the horizon, both ECDSA and EdDSA face a ticking clock. The very signatures securing our transactions and wallets will one day be compromised by quantum computers, exposing funds if we don’t adapt in time. So the question becomes:

How do we bring the same deterministic, user-friendly wallet model provided by BIP-32/39/44 to post-quantum signatures?

Instead of jumping straight into less battle-tested cryptography, a more prudent path is a hybrid HD wallet: one that deterministically derives both classical (e.g., ECDSA) and post-quantum (e.g., Falcon) keys from the same seed phrase. This hybrid approach creates a security bridge between the present day (where the long battle-tested ECDSA sig is sure) and the Q-Day to come. In this blogpost, we present the design a hybrid HD wallet but first, let us see what others have done on this topic.

What others have done

The community has already started paying attention to the challenge of building HD wallets that work with post-quantum (PQ) signatures. A few key questions have started to pop up:

1. Can we build hierarchical derivation for a post-quantum signature scheme?
2. Can we generate different post-quantum signatures from the same seed phrase?

The first question was explored in the QIP-02 proposal, which adapts the hardened derivation logic from BIP-32. It uses deterministic seeds derived from the master key, which are then locally fed into a deterministic PQ key generation algorithm. The second question was tackled in a recent blog post by Project Eleven suggesting the use of BIP-85 to generate independent entropy, that is then used to derive keypairs for different PQ signatures. PQBIP39 from ZKNoxHQ also proposed a solution to generate different 256-bit seeds for multiple signature schemes from a single BIP-39 mnemonic. However, PQBIP39 approach uses the coin_type to branch out seeds according to the different signature schemes.

This naturally leads to a follow-up third question (the main focus of this blog post):

Can we design a hierarchical derivation mechanism that supports both classical and post-quantum signature schemes from the same seed phrase?

This hybrid idea would let users manage both ECDSA and PQ keys within a single deterministic wallet, combining present-day compatibility with future-proof security.

On an orthogonal direction, while QIP-02 handles hardened derivations well (since they can apply to almost any scheme), non-hardened derivations are more complex and depend on the ability to derive public keys without private information. This derivation mechanism is very protocol-dependent and requires tailored approaches to each PQ signing scheme. We list below a non-exhaustive list of papers that address the non-hardened derivation for different schemes (we don't dive into those as this is out of scope for this blogpost).

Reference Signature scheme

• [HLZ24] Hash-and-sign GPV framework (Falcon-like scheme)
• [SR25] Adapted Dilithium
• [ADE+20] qTesla

A note on Falcon

We use Falcon as our main example for PQ signatures, mainly because of its ongoing adoption efforts, such as ethfalcon by ZKNoxHQ, which explores Falcon integration within the Ethereum ecosystem. Besides that, it offers the best tradeoff between signature size and public-key size and relatively efficient signing and verification. Recent work on key generation deterministic implementations, like Thomas Pornin’s ntrugen library, has also shown that Falcon can generate reproducible key pairs from a fixed seed without weakening security [2]. These features make it an attractive candidate for deterministic and hierarchical wallet designs.

However, Falcon also comes with some open questions [3]. The process of deriving a Falcon key pair from a seed is still evolving: NIST’s upcoming FN-DSA standard (the formal Falcon specification) is expected to change the key generation procedure [4], and its first draft has not yet been released. Even Falcon’s co-author Thomas Pornin has warned that current deterministic key generation approaches may not remain backward-compatible once the draft appears. Moreover, NIST has indicated that reproducible key generation may not be guaranteed in the official standard, partly to allow flexibility for different hardware implementations.

In practice, this means that any deterministic or seed-based Falcon wallet needs to lock a specific implementation to ensure reproducibility, at the cost of deviating from future NIST updates. For those reasons, while Falcon is our reference implementation, the ideas explored in this blog post can just as easily extend to other PQ schemes like ML-DSA (Dilithium) where deterministic key generation is already standardized in its FIPS document through KeyGen_internal function (Algorithm 6).

Hybrid HD wallet

Let's start exploring the hybrid hierarchical deterministic derivation proposed in this blog post. The aim is to achieve the following features:

Develop a derivation process that is capable of deterministically generate keypair tree hierarchies for quantum- and non quantum-resistant signatures, while following battle-tested standards that users have familiarity with.

This allows a single BIP-39 mnemonic to deterministically derive key hierarchies for multiple signatures without requiring independent mnemonic seeds. We adopt ECDSA under secp256k1 curve and Falcon-512 as the two signature schemes, but what we present can be generalized to any number of schemes. Also, we hybrid HD procedure uses the following standards: BIP-32, BIP-44, BIP-39, BIP-85 and extends SLIP-10 to PQ signatures.

Overview

In summary, the process to generate a hierarchy of keypairs for both ECDSA and Falcon signatures is as follows. The BIP-39 standard is used to generate a master seed from a mnemonic. Then, the BIP-85 standard is used to generate two child seeds to feed the hierarchical structure of ECDSA and Falcon signatures. The BIP-85 standard internally uses the BIP-32 standard with hardened child key derivation (CKD) to produce those child seeds with the path given by m/83696968'/83286642'/{index}'. Then, the ECDSA branch (index=1) can follow the standard BIP-32 mechanism (hardened or non-hardened) for its hierarchical derivation and the Falcon branch (index=2) follows a SLIP-10 approach.

In other words, we have the following flow:

1. BIP-39 for Master Seed generation.
2. BIP-85 to generate two child seeds using the path m/83696968'/83286642'/{index}':
3. • ECDSA branch (index=1): follows the BIP-32/BIP-44 standards with hardened/non-hardened key derivation.
   • Falcon branch (index=2): follows the SLIP-10 standard adapted to Falcon signatures.

The diagram below describes the hybrid HD approach in a schematic way.

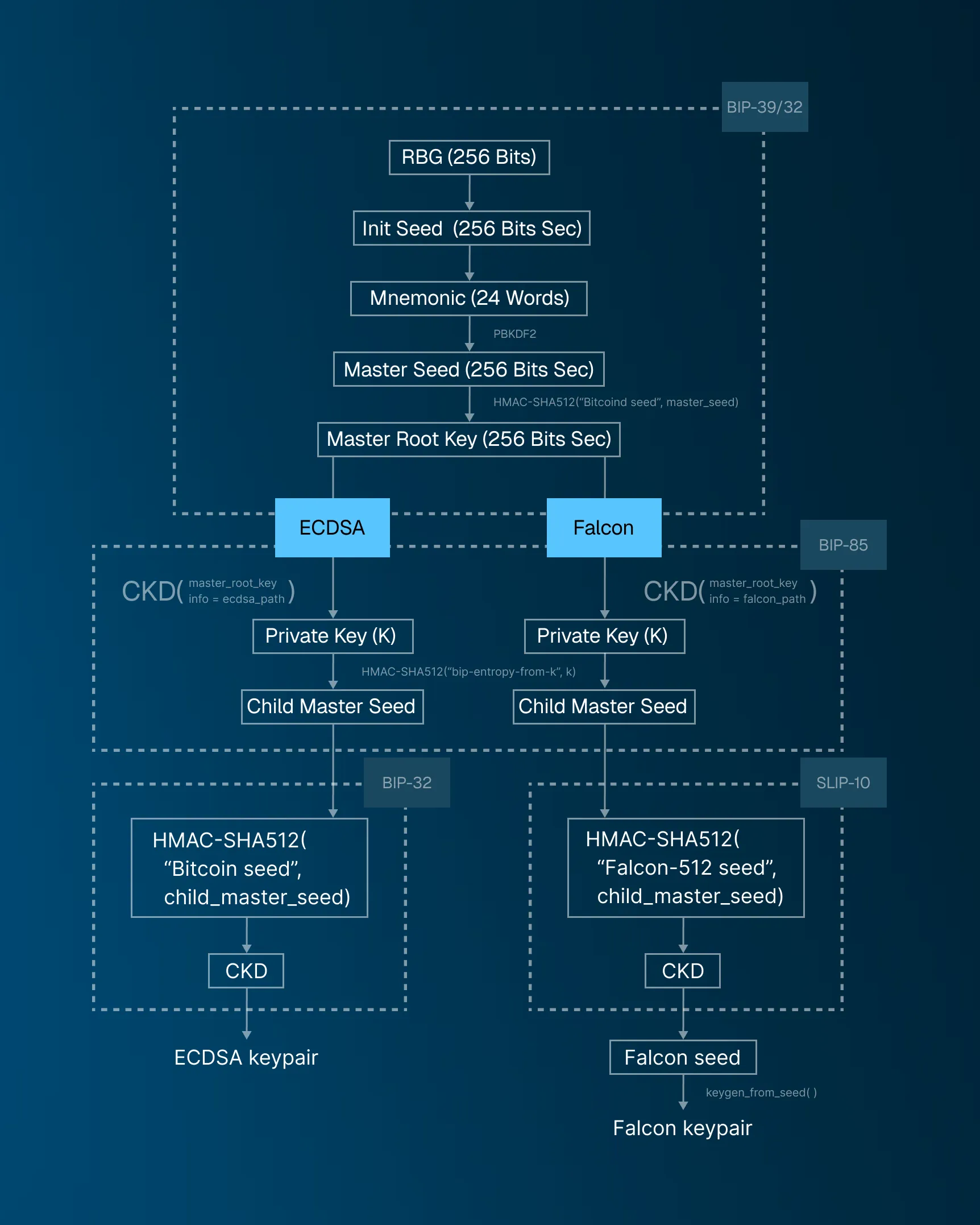
Let's go over each step and comment on the security of our proposal. You can also follow along with its Rust implementation here.

Master seed generation

In order to provide a standard UX for wallet creation, we focus ourselves on the BIP-39 standard to generate a mnemonic wordlist of 24 words, from which a master seed can be derived. We use the exact same master seed derivation mechanism as presented in BIP-39. The following diagram reviews the steps to generate a master seed:

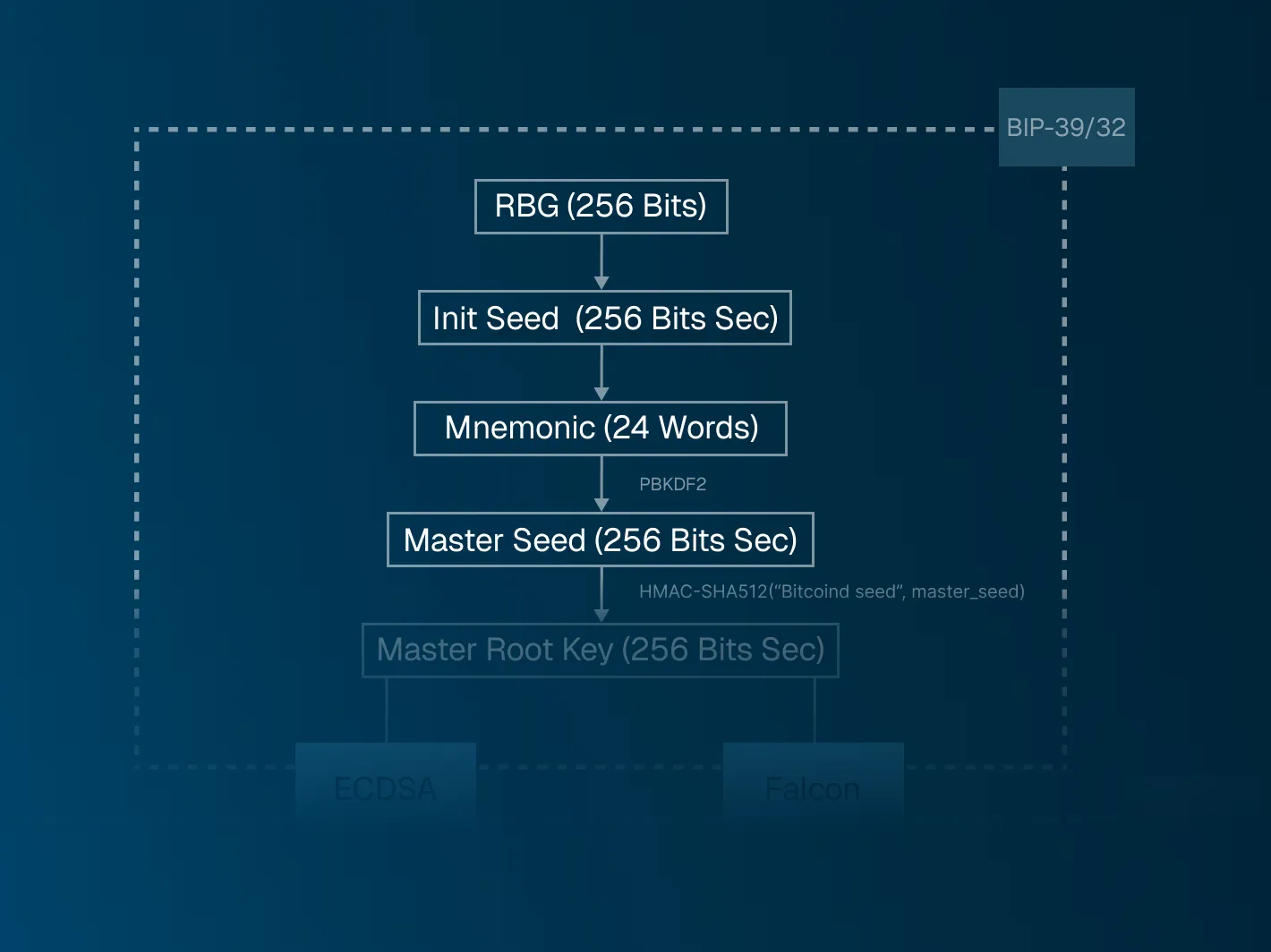
For a more visual description of all steps involved we refer to this material.

Security notes

A conservative choice of parameters allows only mnemonic with at least 24 words. The reason being twofold:

1. Falcon key generation requires a seed with 256 bits of entropy;
2. Grover's algorithm degrades hash-based strength by half.

Let's unpack that below.

NIST compliance

NIST signature approves seeded ML-DSA key generation using an approved random bit generator (RBG) [5]. Although Falcon first draft has not been proposed yet, a similar guideline is expected to apply in case a deterministic key generation is specified. Similar to ML-DSA [5] and as per [6] and [7], the seed for Falcon key generation procedure requires a minimum of 256 bits security.

Therefore, one has to guarantee that the master seed generated in this process can indeed be considered equivalent to a RBG with 256 bits of entropy. The following (very informal) argument supports how that can be achieved. Given RBG strength of 256 bits, mnemonic generation uses SHA256 which preserves the 256 bit security level. Moreover, the PBKDF2 output bit strength is at most the bit security entropy of the password or the PRF strength. Since the entropy of the mnemonic passed as password is 256 bits and SHA512 is used as a PRF, we can conclude that PBKDF2 strength is at most 256 bits.

Grover degradation

From a quantum-threat perspective, all operations involved in BIP-39 are quantum-resistant. It is important to note though that they come with some parameter degradation due to Grover's algorithm and its impact on hash-based cryptography. As a general rule of thumb, if we want to keep the minimum 128-bit security, we need at least 256-bit security in the classical world [8].

Child seeds generation

After having the master seed, we need to derive two child seeds corresponding to both signature types. For that, we follow the approach of this proposal and use the BIP-85 standard.

Let's dive in a bit more to see how it works.

As described in its specification, BIP-85 uses a fully hardened derivation path (by applying a CKD, a chain of functions we will see in the next section) from the BIP-32 master root key. This master root key, according to BIP-32, is computed using HMAC with the string "Bitcoin seed" as key and the master seed as the message. At the end of the chain, BIP-85 additionally applies an entropy derivation function (HMAC-SHA512) to generate the final child seed. The process is summarized below is a schematic way.

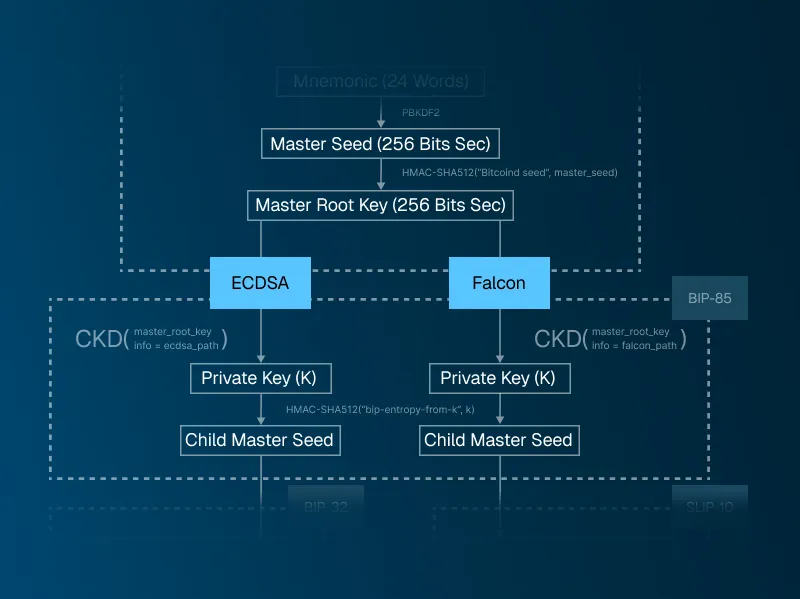
Let's first recall the hardened derivation function used in BIP-32 and then specify the derivation path convention used in our hybrid HD derivation approach for both ECDSA (ecdsa_path) and Falcon (falcon_path) signatures.

Child derivation procedure

Let's see how the child key derivation function (CKD) we mentioned above and defined in the original BIP-32 standard works. This will be a bit mathy but hopefully it is clear enough.

Let's set some notation for clarity. We denote the raw parent key as

kpar, the raw parent chaincode ascpar and index asi. With that in mind we can define the internal hardened functionCKDint((kpar,cpar),i)→(ki,ci) as follows:

1. Check whetheri≥231 (whether the child is a hardened key), output error otherwise.
2. LetI=HMAC−SHA512(key=cpar,data=0x00||kpar||i).
3. SplitI into two 32-byte sequences,IL andIR.
4. Output:(ki,ci)=(IL,IR)

In order to support a hierarchic keychain, we define the child key derivation procedure (CKD) on some path L (a list of ordered indexes) as the recursive call of

CKDintfunction on the elements of L. Let us see an example below.

Example 1 — Path derivation

Imagine the path is given by L=[83696968',83286642',2'], the function

CKD((kpar,cpar),L)→k is computed as follows:

CKDint(CKDint(CKDint((kpar,cpar),83696968'),83286642'),2')=k,

where k is a 512 bit key. As we will see next, this is in fact the path used to generate the Falcon seed.

If you are wondering why we have a prime (') after the numbers, it denotes the hardened path and in practice it adds

231 to the number.

Security notes

In order to use the above process in the generation of the child seeds we need to guarantee two security properties:

1. The CDK process preserves the original entropy (256 bits);
2. Key separation: this guarantees that the newly generated keys are independent from each other, meaning that compromise of one key does not degrade the security of the other keys.

Let's expand the above points below and (very) informally address them.

Key generation process security

The above CDK chained process follows the spirit of HMAC-based Key Derivation Function (HKDF-SHA512) specified in the original [K10] paper and in RFC5869. The HKDF scheme follows an extract-and-expand approach based on some initial secret key material (SKM). The extraction phase uses SKM to generate a pseudo random key (PRK) that is then passed to an expansion function to generate new key material.

We can think of CDK procedure lacking an extraction phase and using the master seed directly as the PRK in the expansion phase. Indeed, as noted in ([K10], Section D, Point 1), since the master seed is already a random string of the length of the HMAC key, one can simply use the master seed as the key to HMAC and jump over the extraction phase. Moreover, the HKDF security property allows the extraction phase to compute HMAC only once during extraction phase. This process is indeed extended in CKD due to the hierarchical nature of the derivation path as CKD computes not only one HMAC but several chained HMACs.

With the above argument we can be relatively convinced that CDK security relies on the security of HKDF analysed in [K10] paper and in RFC5869 [9].

Key separation

For the derivation of the child seeds it is important to guarantee that any material leaked in one branch does not affect the security of the other branch. This key separation principle is guaranteed by the key derivation function (KDF) mechanisms defined in NIST SP 800-108. Since HKDF is a valid KDF specified in the document, and CDK mechanism breaks down to HKDF (check previous subsection argument), we can be convinced that the CDK process achieves the key separation principle.

Derivation path convention

Ok. After learning how the chained CDK procedure works, let us now see the structure of the derivation path for our design.

In BIP-85 a private key can be derived from the BIP-32 master root key using a fully hardened derivation path. The derivation path follows the convention:

m/83696968'/{app_no}'/{index}',
where {app_no} is the path for the application, {index} is the index, and the prime ' is used to refer to a hardened derivation (i.e., as we saw in the Example 1 above, in practice it adds

231to the corresponding number).

The hybrid HD derivation app number is app_no = 83286642, standing for Tectonic written in a T9 keyboard. ecdsa-secp256k1 signature is given index=1 and falcon-512 signature is given index=2.

We recall that the hardened derivation path does not use an ECC specific construction as the

kparis passed as raw bytes to the HMAC in the Data field. Therefore, this process can be applied to a generic derivation mechanism.

Child master seed derivation

Finally! Now, we can finish with the BIP-85 standard to get the final seed!

The output of CKD denoted by k is passed to HMAC-SHA512("bip-entropy-from-k", k) to extract new entropy. The result (child_master_seed) is our child master seed for the derivation of either ECDSA or Falcon keypairs.

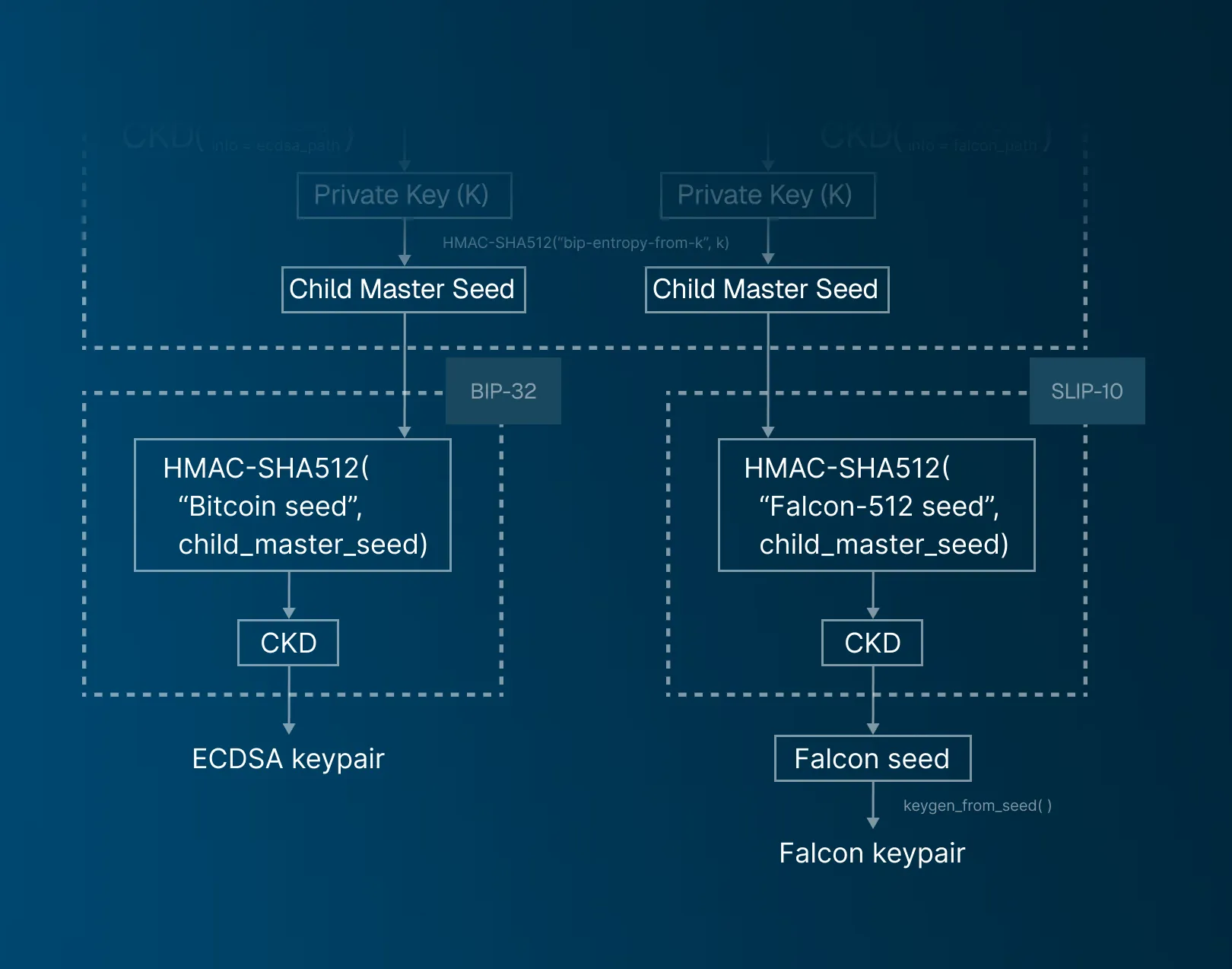
HD keychain

The entropy derived from BIP-85 procedure described above for the two branches can then be used as the seed for the generation of two keychains.

The ECDSA branch can follow the traditional BIP-32 hierarchical derivation with either hardened or non-hardened derivation paths. The Falcon branch (or any other PQ signature) follows a hardened derivation path proposed in SLIP-10 for universal key derivation. We adopt a similar approach to ed25519 signature with a tailored domain separator string "Falcon-512 seed", used in the master key generation step.

As we discussed in the motivation section, the Falcon original proposal does not provide an out-of-the-box rerandomization key technique, which is the feature required for a non-hardened derivation path.

Below we show a schematic diagram with the hierarchical derivation used by the two branches.

Conclusion

In summary, our hybrid hierarchical deterministic wallet shows how a single BIP-39 seed phrase can deterministically generate both classical (ECDSA) and post-quantum (Falcon-512) key hierarchies, maintaining usability while preparing for future quantum threats. By leveraging standards like BIP-32, BIP-39, BIP-44, BIP-85, and SLIP-10, the design ensures strong key separation and preserves a user experience consistent with existing wallet workflows. While Falcon serves as our main example, the approach is flexible and can be extended to other post-quantum schemes, such as ML-DSA.

An open-source Rust implementation is available in our Bedrock repo for the community to explore and build upon. We also have its specification in the hhd-spec repo.

References & comments

[1] The day quantum computers will become powerful enough to break the classical cryptographic assumptions that protect today’s blockchains.
[2] Also, as commented by Bas Westerbaan on PQC Google group (22.12.2022): For every scheme it's possible to make key generation deterministic by replacing "randombytes()" calls by calls to a XOF that has been seeded by the "private key seed".
[3] Along with some implementation challenges as commented by Cloudflare blog post.
[4] As commented by Dustin Moody on PQC Google group (28.08.2025): our current draft includes tweaks to the Gaussian sampler in Keygen made in consultation with the Falcon team, including an allowance for fixed point arithmetic – it’s not identical to either the original Falcon submission or to HAWK, though.
[5] FIPS 204 section 3.6.1
[6] Falcon original proposal page under "Performance" section: Private key size (not listed above) is about three times that of a signature, and it could be theoretically compressed down to a small PRNG seed (say, 32 bytes), if the signer accepts to run the key generation algorithm every time the key must be loaded.
[7] Current implementations use 32 byte seed which is enough for Falcon-512 but arguably not for Falcon-1024 where a 40-byte seed should be passed (check [P19] last paragraph of Section 5.1).
[8] SHA256 was recently analysed in [GM19] Table 1 and it provides a quantum security of 166 bits due to Grover's algorithm.
[9] In [DEF+21] the authors actually show a slight degradation in the security strength of BIP-32 from 128 bits to 91 bits. It would be interesting to have a more formal analysis of BIP-85 procedure and its relation to PQ key generation considering [DEF+21] result.